Tässä osassa katsotaan hieman neuroverkon sisälle, sen rakenteeseen ja toimintaan. Tässä vaiheessa lähdemme liikkeelle yksittäisestä keinotekoisesta ”hermosolusta” ja kokeilunhaluiset voivat myös itse yrittää kokeilla kuinka sellainen toimii ja oppii. Katsomme myös kuinka näistä ”soluista” kootaan kerroksia ja kerroksista edelleen suurempia verkkoja.
Neuroverkon perusosanen, keinotekoinen ”hermosolu”, perseptroni, laskee käytännössä syötteiden i painotetun summan. Oppivan siitä tekee se että solu pystyy oppimaan painokertoimet w esimerkkien pohjalta.
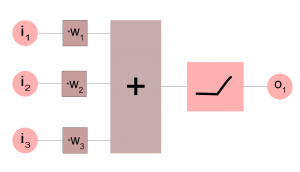
Syötteet ovat numeerisia (esim. 0.4 tai -0.32) ja ne voivat siksi kuvata erilaisia reaalimaailman suureita, mittaustuloksia tai vaikka pörssikursseja. Ulostulo on myös luonnostaan numeerinen. Jos verkosta halutaan ulostulona binäärinen tieto (tosi/epätosi, oikein/väärin, kunnossa/hälytys), voidaan solun perään lisätä aktivaatiofunktio, joka esimerkiksi antaa hälytyksen kun summauksen arvo ylittää tietyn kynnysarvon (eli matemaattisesti katsoen kyseessä on askelfunktio, jonka arvo menee nollasta ykköseksi kun syöte ylittää kynnysarvon).
Solun ulostuloon lisätäänkin käytännössä lähes aina jokin epälineaarinen aktivaatiofunktio, jolloin solu ei vain laske syötteiden painotettua summaa vaan tekee myös päätöksen. Kuvassa näkyvä aktivaatiofunktio korvaa negatiiviset arvot nollalla (tätä kutsutaan nimellä ReLU ja se on hyvin yleisesti käytetty).
Katsotaanpa käytännössä, apuna torch-ohjelmakirjasto. Kokeiluihin suosittelen Ubuntua tai vastaavaa Linux-jakelua, johon torch voidaan asentaa näiden ohjeiden avulla. Torchia voi käyttää paitsi ajettavissa ohjelmissa myös komentotulkin kautta jolla on kätevä tehdä pienimuotoisia kokeiluja. Seuraavaksi näytän miten th-komentotulkissa voidaan luoda yksisoluinen neuroverkko ja kokeilla sen koulutusta.
Ensin luomme neuroverkon jossa on kolme syötettä ja yksi ulostulo, siis käytännössä yksi ”solu”. Torchin neuroverkoissa solun summauksessa voi olla mukana ns. bias, laitamme sen nyt nollaksi. Painokertoimet asetamme satunnaisiksi ja katsomme mitä niiden arvoiksi tuli.
th> require 'nn' th> net = nn.Linear(3,1) th> net.bias[1] = 0 th> net.weight = torch.rand(1,3) th> print(net.weight) 0.6977 0.6862 0.8461 [torch.DoubleTensor of size 1x3]
Seuraavaksi luomme syötteen kolmesta luvusta, syötämme sen neurosolullemme ja katsomme mitä saamme tulokseksi.
th> input = torch.Tensor({0, 0.5, 0.2})
th> output = net:forward(input)
th> print(output)
0.5123
[torch.DoubleTensor of size 1]
Oletetaan nyt että tällä syötteellä haluttu tulos olisi 0.3. Tulos on nyt liian suuri, laskemme poikkeaman halutusta ja käskemme yksisoluista verkkoamme korjaamaan painoarvojaan siihen suuntaan että lopputulos olisi lähempänä oikeaa.
th> dOut = output - 0.3 th> net:backward(input, dOut) 0.1481 0.1457 0.1797 [torch.DoubleTensor of size 3] th> net:updateParameters(0.1)
0.1 on tässä oppimistahti. Yksittäisen esimerkin perusteella ei kannata laittaa painoarvoja kokonaan uusiksi (oppimistahti = 1). Käytännössä haetaan aina jonkinlaista optimia joka antaa hyviä tuloksia kaikilla koulutusaineiston esimerkeillä. Katsotaan nyt mitä painoarvoille on tapahtunut ja mitä saamme tulokseksi samalla syötteellä:
th> print(net.weight) 0.6977 0.6756 0.8418 [torch.DoubleTensor of size 1x3] th> output = net:forward(input) [0.0002s] th> output 0.4849 [torch.DoubleTensor of size 1]
Nähdään että tulos on siirtynyt lähemmäksi haluttua. Jos nyt toistetaan koulutusta päästään asteittain lähemmäksi oikeaa tulosta.
th> net:backward(input, dOut) 0.1481 0.1435 0.1788 [torch.DoubleTensor of size 3] th> net:updateParameters(0.1) th> print(net:forward(input)) 0.4302 [torch.DoubleTensor of size 1]
Koulutuksen toistamisessa yhdellä ja samalla syötteellä ei kuitenkaan ole juuri järkeä, käytännössä koulutus tehdään aina sopivalla joukolla esimerkkejä. Huomaa myös että tässä emme vielä käyttäneet mitään aktivaatiofunktiota.
Näin siis yksittäinen ”solu” toimii. Jos tarvitsemme enemmän ulostuloja, voimme koota verkon useammasta solusta näin. Kuvassa i kuvaa syötteitä ja o yksittäisiä soluja. Meillä on nyt siis kaksi solua, jotka kumpikin saavat saman syötteen, mutta tuottavat ulostulonsa itsenäisesti.
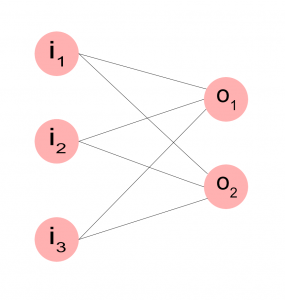
Torchissa tämmöinen verkko syntyy yhtä helposti kuin yhden solunkin tapauksessa. Syöte koostuu edelleen kolmesta luvusta, tulos koostuu nyt kahdesta lukuarvosta.
th> net = nn.Linear(3,2)
th> net.weight = torch.rand(2,3)
th> net.bias = torch.Tensor():resizeAs(net.bias):fill(0)
th> print(net.weight)
0.0186 0.0803 0.3084
0.0921 0.9462 0.3576
[torch.DoubleTensor of size 2x3]
th> input = torch.Tensor({0, 0.5, 0.2})
th> output = net:forward(input)
th> print(output)
0.1018
0.8292
[torch.DoubleTensor of size 2]
Nyt olemme luoneet rinnakkaisista soluista kerroksen, jonka syötteen dimensio on 3 ja tuloksen 2. Mutkikkaammat ongelmat voivat tarvita useamman päällekkäisen kerroksen jolloin tieto jalostuu kahdessa vaiheessa, syötteistä i välikerrokseksi h (hidden layer) ja siitä edelleen ulostuloksi o. Tässä on nyt oleellista, että sekä h-kerros että i-kerros tekevät summauksen lisäksi jonkinlaisen päätöksen (sisältävät aktivaatiofunktion).
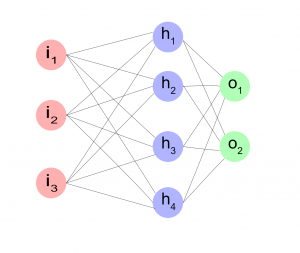
Tämä syntyy torchissa näin. Huomaa kuinka lisäämme epälineaarisen ReLU-funktion kummankin kerroksen jälkeen.
th> net = nn.Sequential() th> net:add(nn.Linear(3,4)) th> net:add(nn.ReLU()) th> net:add(nn.Linear(4,2)) th> net:add(nn.ReLU())
Tässä osassa olemme nyt käsitelleet yksinkertaisia neuroverkkoja, joilla voidaan käsitellä numeerista tietoa ja tehdä niistä päätelmiä joiden muoto on myös numeerinen, josta voidaan haluttaessa myös tehdä on/off -tieto. Olemme myös nähneet kuinka verkon painokertoimet muuttuvat koulutuksen aikana. Seuraavassa osassa katsomme miten verkko pystyy käsittelemään kuvamuotoista tietoa.



